
之前的工作
RNN 存在长期依赖问题(隐含信息一直传递到后面会消失),且无法并行
LSTM 通过遗忘门,输入门,输出门解决长期依赖问题,但是还是无法并行
Transformer仅仅依赖注意力机制(Attention),不需要考虑两个词离得多远,且能实现并行
模型架构
输入$(x_1,x_2,…,x_n)$,编码器输出$(z_1,z_2,…,z_n)$,其中$z_t$是$x_t$的嵌入向量,输入到解码器,根据$y_1$到$y_{t-1}$以及$z_t$输出$y_t$
每一步都是自回归的(编码的时候可以看到一整个句子,但是在解码的时候只能看到已经生成好的句子,叫做自回归auto-regressive,它将时间序列的当前值表示为过去若干个值的线性组合)
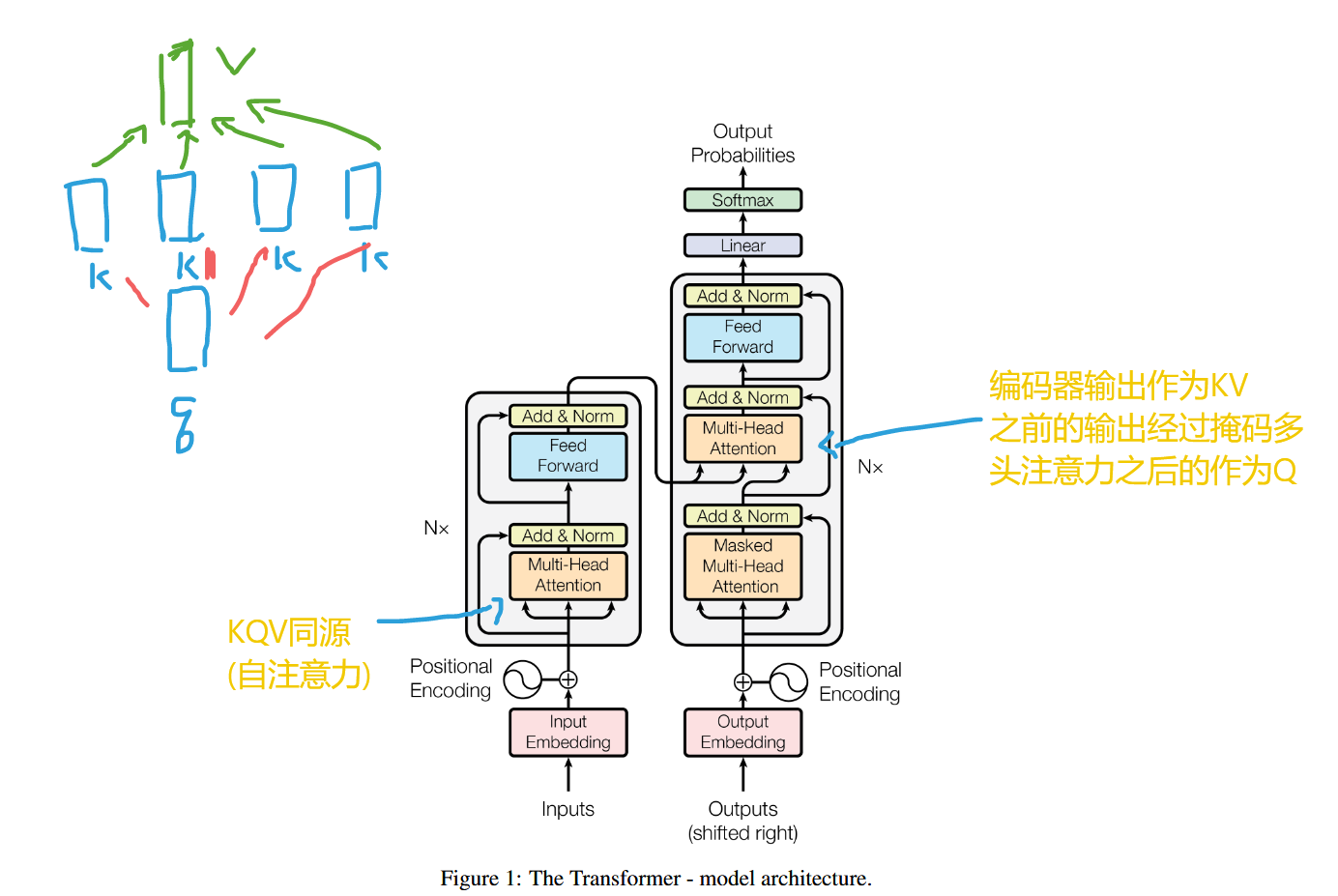
编码器
N=6,每一层有两个子层:多头注意力层和前馈神经网络层,每个子层后面还有一个残差网络和层归一化(Add & Norm),即每个子层的输出是
$LayerNorm(x + Sublayer(x))$
$d_k = 512$
LayerNorm & BatchNorm
| 归一化类型 | 归一化维度 | 适用场景 |
|---|---|---|
| BatchNorm | 对同一特征通道跨样本(Batch维度)归一化 | CNN等固定输入结构的模型 |
| LayerNorm | 对同一样本的所有特征(Channel维度)归一化 | RNN、Transformer等变长序列模型 |
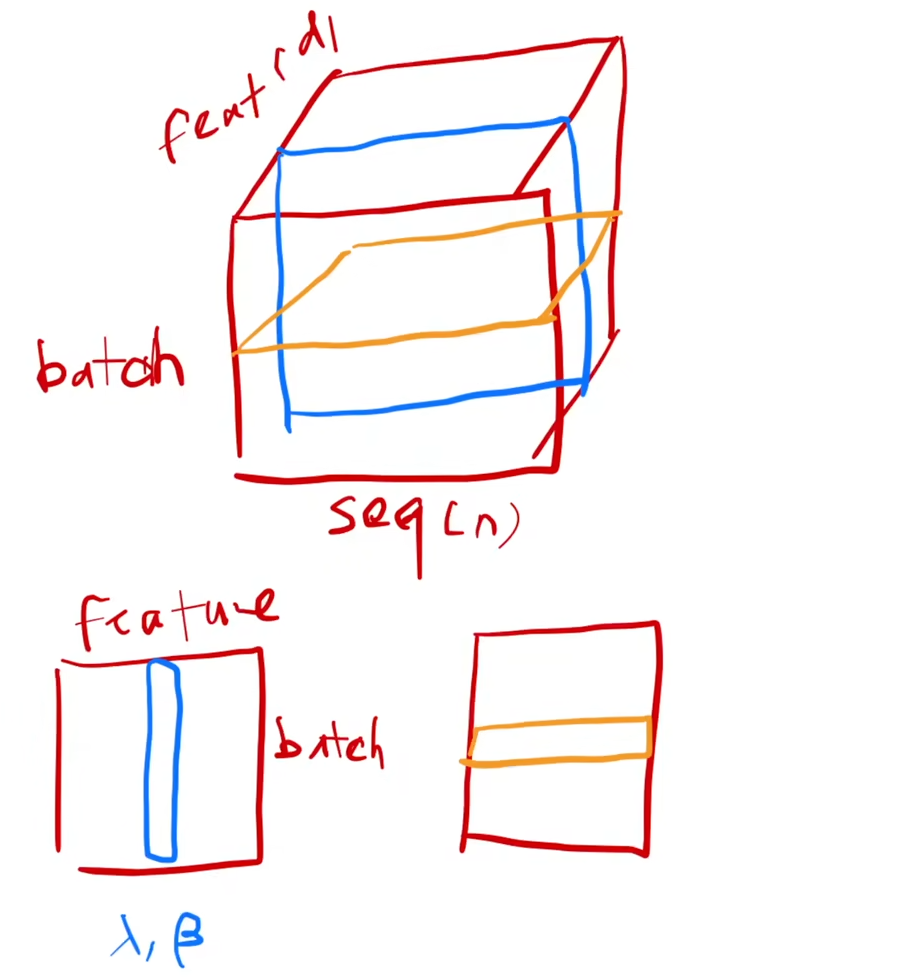
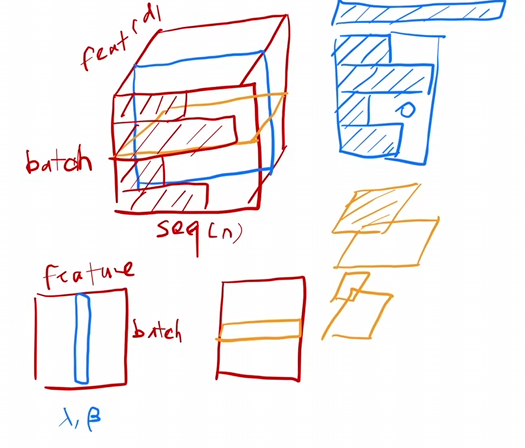
蓝色是batchnorm,黄色是layernorm
BN对每一个特征在一个小批量(mini-batch)计算均值和方差,然后对整个小批量进行归一化,推理的时候要记录全局的均值和方差
由于每个seq的长度可能不一样,导致对不同seq的某个feature进行归一化的时候容易出现抖动(特别是batch比较小的时候)
而LN对每一个样本在一个小批量(mini-batch)计算均值和方差,然后对整个小批量进行归一化,训练和推理行为一致
都是在每个样本自身里面归一化,所以比较稳定
解码器
N=6,在输入添加一个掩码多头注意力,和encoder有两个一样的子层
此外多了一个掩码多头注意力层
注意力机制
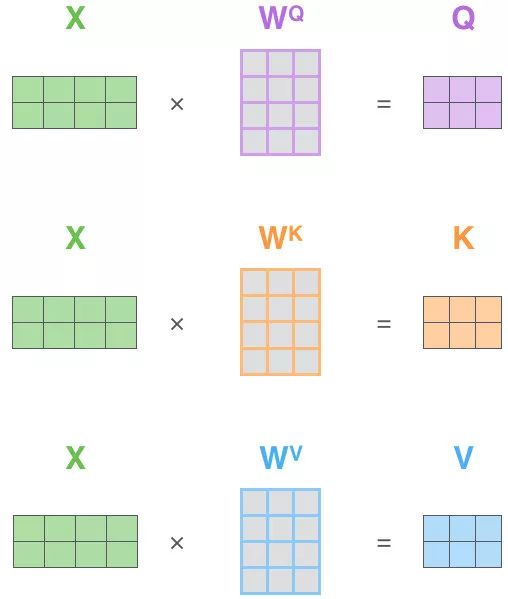
通过Q,K,V,计算两个词的相似度
Transformer采用自注意力机制
Scaled Dot-Product Attention
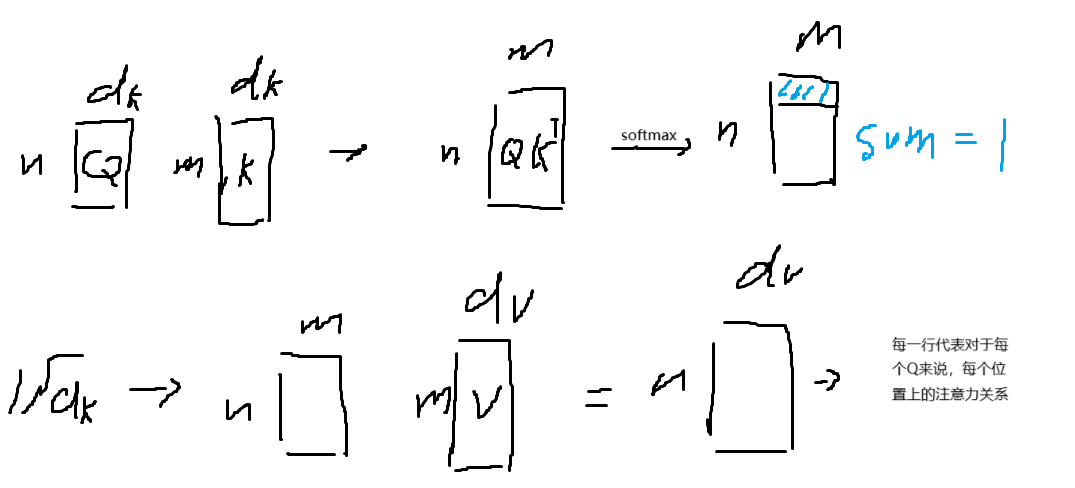
Q,K的维度都是$d_k$,V的维度是$d_v$
Q,K做内积,再除以$\sqrt{d_k}$,做一层softmax(对每一行,dim=1)就是V的权重
$Attention(Q,K,V) = softmax( \frac{QK^T}{\sqrt{d_k}} )V$
为了防止dk过大或者过小,使得softmax的值趋于0或者1导致softmax的梯度很小减慢训练速度,所以处理$\sqrt{d_k}$
多头自注意力机制
h=8
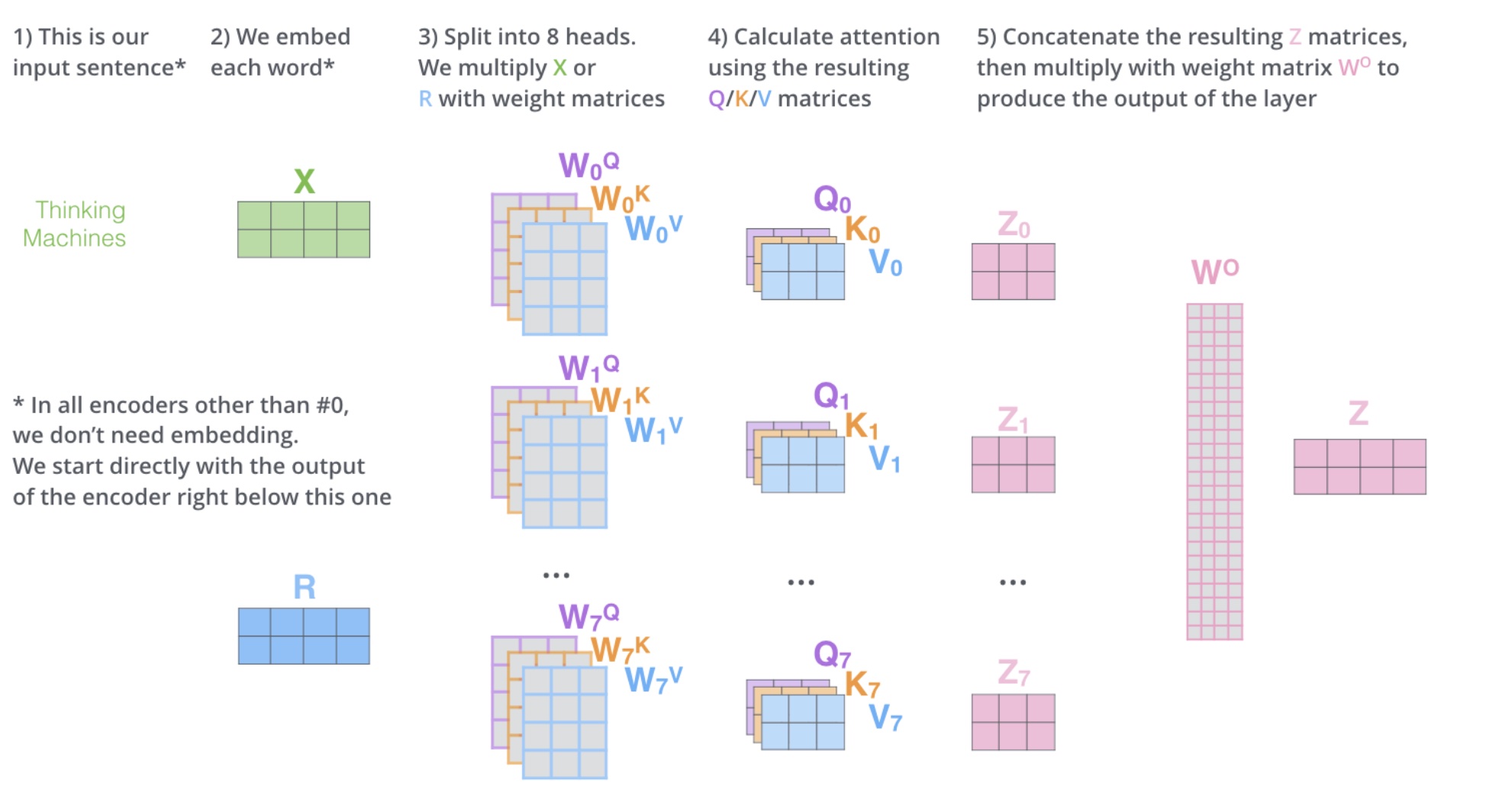
多头相当于把原始信息 Source 放入了多个子空间中,也就是捕捉了多个信息,对于使用 multi-head(多头) attention 的简单回答就是,多头保证了 attention 可以注意到不同子空间的信息,捕捉到更加丰富的特征信息。
也就是先对QKV进行投影到一个新维度,进行h次注意力计算,把h个结果拼接起来,通过Linear投影回原来的维度
例如$z_i \in R^{2×3}$,拼接起来就是$R^{2×24}$,再内积$W^O \in R^{24×4}$,最终得到$Z \in R^{2×4}$,通过这样操作,可学习的参数就会大大增加
投影参数矩阵
$W^Q_i \in R^{d_{model}×d_k}$
$W^K_i \in R^{d_{model}×d_k}$ ,
$W^V_i \in R^{d_{model}×d_v}$
$W_O \in R^{ {hd_v}×d_{model} }$
dk = dv = dmodel/h = 64
计算消耗和一次注意力差不多,但是能学到更多的信息。
masked多头注意力
在计算的时候,只考虑前面出现过的,所以他的输入是output embedding
计算出来的结果作为上面的input的Q

Encoder-Decoder注意力层
KV来自编码器,Q来自解码器
前馈神经网络
由两个线性回归和一个ReLU的全连接层
$FFN(x) = ReLU(xW1 + b1)W2 + b2$
内层的维度2048
512->(W1)2048->(W2)512
(先由attention计算相似度拿到感兴趣的信息,语义空间在MLP隐藏层里面转化为2048维)
嵌入层和Softmax
在两个嵌入层的矩阵参数选择一样的,然后再乘以$\sqrt{d_{model}}$
(可能由于L2正则化权重值很小,下面还要和位置编码相加,保证两个向量的scale差不多,所以乘)
位置编码
由于 Attention 值的计算最终会被加权求和,也就是说两者最终计算的 Attention 值都是一样的,进而也就表明了 Attention 丢掉了 X1的序列顺序信息。
Attention自己是没有包含时序的信息的
所以要有位置编码
$PE(pos,2i) = sin(pos/10000^{2i/d_{model}})$
$PE(pos,2i + 1) = cos(pos/10000^{2i/d_{model}})$
PE都在[-1,1]且$PE_{pos_k}$是$PE_{pos}$的线性组合
某个单词的位置信息是其他单词位置信息的线性组合,这种线性组合就意味着位置向量中蕴含了相对位置信息。
$X_{final_embedding}=Embedding+PositionalEmbedding$
性能
| Layer Type | Complexity per Layer | Sequential Operations | Maximum Path Length |
|---|---|---|---|
| Self-Attention | O(n2 · d) | O(1) | O(1) |
| Recurrent | O(n · d2) | O(n) | O(n) |
| Convolutional | O(k · n · d2) | O(1) | O(logk(n) |

